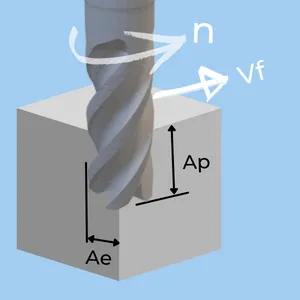
In milling, the depth of cut is two-dimensional. The Radial depth of cut (AE or RDOC) is the length that the tool engages a workpiece perpendicular to its axis direction. The Axial depth of cut (AP or ADOC) is the length in its axis direction. They are both measured perpendicular to the table feed direction.
The two parameters are interlinked, and finding the best value for each of them and the proportion between them is critical to achieving a balanced milling process (Productivity, Safe process, and tool-life)
Table of Contents
Axial Depth of Cut (Cut Depth)

- The Axia depth of cut is also called Stepdown and Cut depth.
- It is designated by ap or ADOC.
- The maximum possible depth depends mainly on the cutter’s diameter.
- For large diameter cutters (Above 3/4″, 20 mm), It is up to 4D (4 times the diameter).
- For small diameter cutters (Below 1/8″, 3 mm) it is up to 10D.
Optimal Cut Depth Calculators
The typical (and wrong!) opinion is that the larger the depth, the more vibrations will be in the cut. However, there are optimized cut depths that create minimum vibrations.
Optimal Depth of Cut Calculator
The calculator below shows the cut depths (ap), which yield the least vibrations. (Read below why)
Optimal Milling Cutter for a given Depth
The calculator below shows the diameters and helix angle combinations, which yield the least vibrations for a given depth. (Read below why)
Reducing vibrations by optimizing the depth of cut
The cutting force during a milling operation depends on the depth of cut, chip load, raw material, cutting angles, and the total length of engagement between the cutting edges of the endmill and the material being cut. All the parameters stay constant throughout the operation except for cutting-edge engagement. The length of the helix, which is in contact with the material, varies as the cutter rotates.
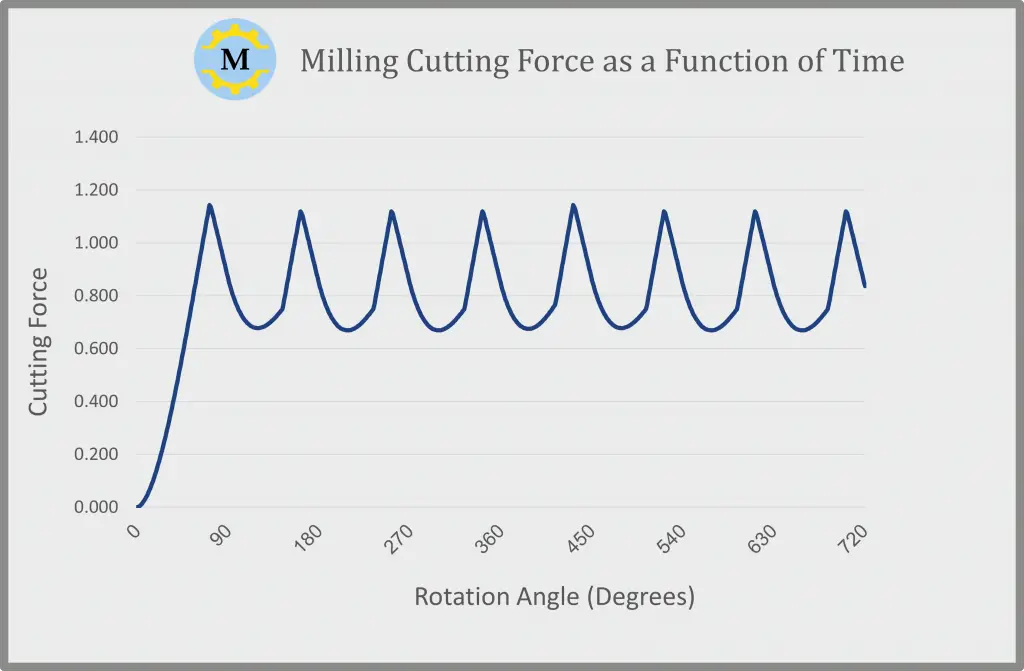
Therefore, a typical graph for the cutting forces acting on a solid carbide endmill as a function of time (or rotation angle) is like shown here.
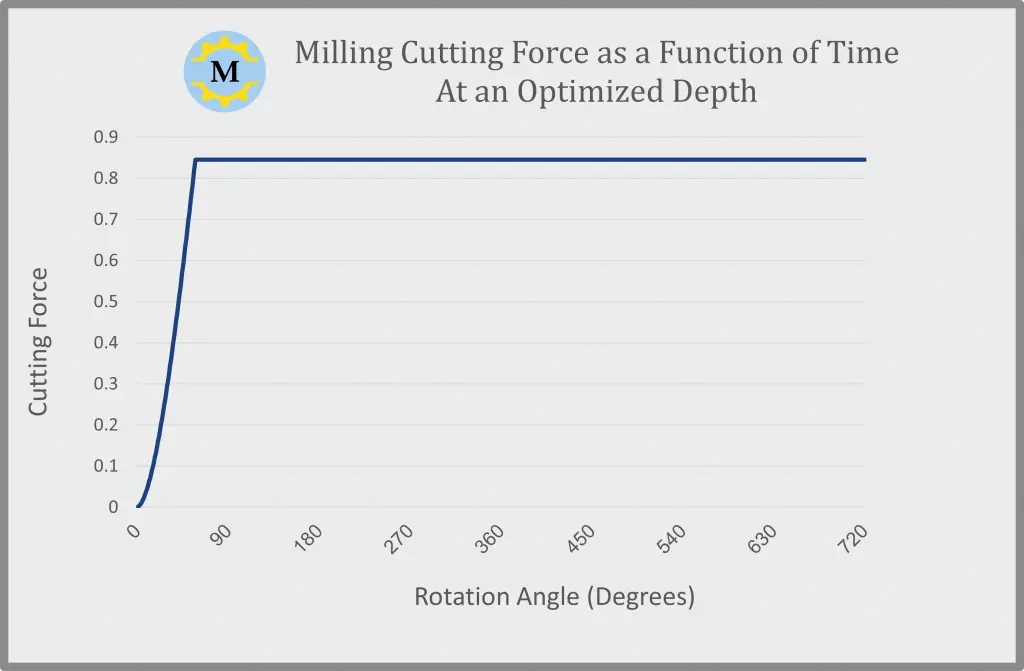
However, specific combinations of diameters, number of flutes, helix angles, and depth of cut yield a constant contact length independent of the rotation angle, therefore, a constant force.
Since the diameter, helix angle, and flute count of the milling cutter can not be changed. We can find an optimal cut depth that will yield a constant cutting force:
You can use our above calculator to find out this depth of cut. All the multiples of this depth will also yield constant force.
When you machine with a constant force, you will get less vibrations, a better surface finish, and a longer too-life.
You can also use this theory in another effective way. Suppose you have a mass-production job and must constantly machine at a certain depth. If you reverse the formulas, you can find specific combinations of diameter, flute count, and helix angles to yield constant force and smooth machining. The result will be non-standard figures. But it may be well worth designing and purchasing a special cutter according to these parameters for a mass-production job.
You can use our above calculator to find out the optimal milling cutter geometry for your required depth of cut.
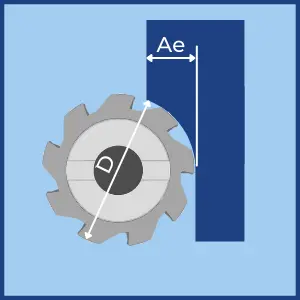
Radial Depth of Cut (Cut Width)
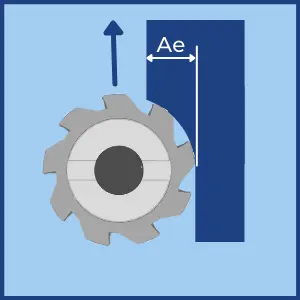
- The Radial depth of cut is also called Stepover and Cut Width.
- It is designated by ae or RDOC.
- The maximum possible radial depth is the cutter’s diameter.
- When the radial depth is larger or equal to the cutter’s radius, the chip load is similar to the feed per tooth.
- The chip load is reduced for smaller cut widths because of the chip thinning effect. (See below)
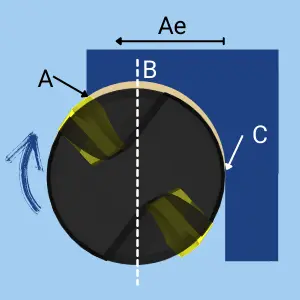
Chip Thinning Effect
- In a milling operation, the Chip Thickness varies between the point of entry (A) and the Point of Exit (C).
- When the Radial Depth of Cut is greater or equal to the cutter’s radius, The maximum Chip thickness equals the Feed Per Tooth.
- When the radial depth of cut is smaller than the cutter’s radius (Point B), the maximum chip thickness gradually decreases even though the feed per tooth remains the same.
- This phenomenon is called Chip Thinning.
Chip Thinning allows dramatic productivity gain since you can multiply the Feed by the Chip Thinning Factor (RCTF) while keeping the Chip Load within the recommended range! Learn more about it in our detailed guide about chip thinning
\( \huge \frac{1}{\sqrt{1-\left ( 1 – 2 \times \frac{Ae}{D} \right )^{2}}} \)









