This page is a collection of basic Turning calculators and formulas. Each topic includes an online calculator, formulas, and explanations. For easier use, you can toggle between the units (Metric/Imperial) and choose to view everything or only the calculators (Explanations and formulas will be hidden)
This page includes only elementary calculators. For more advanced calculators, there is a separate page for each. Go to the Machining Calculators Page for the complete list.
Choose a Turning Calculator
Cutting Speed Calculator and Formulas
How to calculate the cutting speed in a turning operation based on the workpiece diameter and spindle speed

- d – Turned Diameter
- n – Spindle Speed
- Vc – Cutting Speed
Theory
Cutting speed is the relative linear velocity between the tip of the turning insert and the workpiece. It is the product of the rotation speed of the workpiece (Spindle speed) and the circumference at the smallest diameter of the cut.
Important Note: Pay attention that the diameter d is the smallest diameter in the operation. In external turning, it is smaller than the outer diameter, and in internal turning, and larger than the inner diameter!
\( \large d=OD{ }-{ }2 \times{ }a_p \text{ (External turning)} \)
\( \large d=ID{ }+{ }2 \times{ }a_p \text{ (Internal turning)} \)
\( \large \text{Circumference = }C = 2 \times \pi \times r = \pi \times d \)
\( \large Vc= n \times C \)
Power Tip – Use our Speed and Feed Calculator to get the recommended cutting speed based on dozens of parameters!
Formula in metric units
- d – [mm]
- n – [rpm] (Revolutions per minute)
- Vc – [m/min]
Formula in Imperial units
- d – [Inch]
- n – [rpm] (Revolutions per minute)
- Vc – [SFM] (Surface feet per minute)
Spindle Speed Calculator and Formulas
How to calculate the spindle speed of a lathe based on the turned diameter and cutting speed

- d – Turned Diameter
- n – Spindle Speed.
- Vc – Cutting Speed
Theory
The turning inserts catalog or our experience tells us the cutting speed we need to use for a given application. On the other hand, the CNC lathe is limited by its maximum spindle speed. Therefore it is common that we need to compute the spindle speed out of a given cutting speed to ensure that the speed we want to run at is within the machine’s limit. It is calculated by dividing the cutting speed by the turned diameter circumference.
Important Note: Pay attention that the diameter d is the smallest diameter in the operation. In external turning, it is smaller than the outer diameter, and in internal turning, it is larger than the inner diameter!
\( \large d=OD{ }-{ }2 \times{ }a_p \text{ (External turning)} \)
\( \large d=ID{ }+{ }2 \times{ }a_p \text{ (Internal turning)} \)
\( \large \text{Circumference = }C = 2 \times \pi \times r = \pi \times d \)
\( \large n= \huge \frac{V_c}{C} \)
Power Tip – Use our Speed and Feed Calculator to get the recommended cutting speed based on dozens of parameters!
Formula in metric units
- d – [mm]
- n – [rpm] (Revolutions per minute)
- Vc – [m/min]
Formula in Imperial units
- d – [Inch]
- n – [rpm] (Revolutions per minute)
- Vc – [SFM] (Surface feet per minute)
Metal Removal Rate Calculator and Formulas
The MRR Calculator determines the volume of material removed per minute by a turning operation at certain cutting conditions.

- Ap -Depth of cut
- Fn – Feedrate
- Vc – Cutting Speed
- Q – MRR
Theory
The Metal removal rate (MRR) is measured in cubic inches (Or cubic cm) per minute and indicates how much material is machined in one minute at a set of cutting conditions. In turning, it is the product of the Feedrate, depth of cut, and cutting speed. Learn more in our in-depth Metal Removal Page. MRR is used for two purposes:
- Comparing the productivity between two sets of cutting conditions.
- Estimating the required machine power consumption.
Formula in metric units
- Fn – Feedrate [mm/rev]
- ap -Depth of cut [mm]
- Vc – Cutting Speed [m /min]
- Q – Metal Removal Rate [cm3/min]
Formula in Imperial units
- Fn – Feedrate [IPR]
- ap -Depth of cut [inch]
- Vc – Cutting Speed [SFM]
- Q – Metal Removal Rate [inch3/min]
Machining Time Calculator and Formulas
Determine how long it takes to turn a given length at certain cutting conditions.

- Fn – Feedrate
- Vc – Cutting Speed
- n – Spindle Speed
- l – Length
Theory
Since the feddrate for turning is expressed in distance per one full spindle rotation, the linear speed in the feed direction is the product of the feedrate and the spindle rotation speed:
\( \large V_f = n \times F_n \)
Hence the cutting time is the length divided by the linear speed:
\( \large T = \huge \frac{l}{V_f} = \frac{l}{F_n \times n}\)
However, in most cases, we know the cutting speed, not the spindle speed. If we substitute n with the spindle speed formula, we can calculate the machining time directly:
\( \large n = \huge \frac{12 \times V_c}{\pi \times d} \)
\( \large T = \huge \frac{l \times \pi \times d}{12 \times F_n \times V_c} \)
\( \normalsize \text {(in mentric units the constant 12 shoud be repalced with 1,000)} \)
Important Note: If you use the formula based on cutting speed, you must ensure that the speed is not limited by the machine’s maximum RPM. If that is the case, use the formula based on the spindle speed!
Formula in metric units
- Fn – Feedrate [mm/rev]
- Vc – Cutting Speed [m /min]
- d – Turned Diameter [mm]
- T – Turning Machining Time [min]
Formula in Imperial units
- Fn – Feedrate [IPR]
- Vc – Cutting Speed [SFM]
- d – Turned Diameter [Inch]
- T – Turning Machining Time [min]
Surface Finish Calculator and Formulas
Determine the theoretical surface roughness that can be achieved per a given pair or insert corner radius and feedrate.
Power Tip – Below is a simple calculator with basic explanations. For advanced surface finish calculators with detailed explanations, Go Here
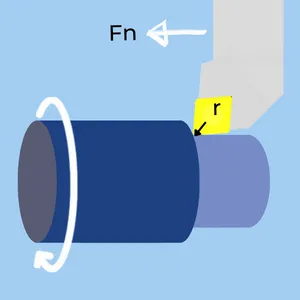
- Fn – Feedrate
- r – Corner Radius
- Ra – Surface Finish
Theory
The surface roughness of the turning operation depends on the feedrate and the insert corner radius. A lower feedrate improves the surface finish, as does a larger corner radius.
Power Tip – The feedrate is squared in the formula and therefore has a more significant influence. When you need to improve the surface quality, start by reducing the feedrate
\( \large R_a = K \times \huge \frac {F_n^{2}}{r} \)
\( \normalsize \text {(K is a constant that depends on the units used)} \)
This formula provides the best theoretical surface finish at optimal conditions. The actual surface quality depends on additional factors such as stability and cutting edge wear.
Formula in metric units
- Fn – Feed rate [mm/rev]
- r – Corner Radius[ mm]
- Ra – Surface Finish [μ]
Formula in Imperial units
- Fn – Feed rate [IPR]
- r – Corner Radius [Inch]
- Ra – Surface Finish [μ Inches]









