Knurling: Calculator & Formulas (Diameters, Speed & Feed)

Table of Contents

Knurling Calculator

Determines the required blank diameter for getting the correct diameter after knurling.
Knurling Speeds and Feeds.

What is Knurling?

Knurling is a manufacturing operation, performed on a lathe, that copies a pattern from a knurling wheel onto a round workpiece. It is mainly used for:

Increasing the friction of an area on a part for easier human grip. For example, a Micrometer Knob.
Improving the grip of a metal part assembled into plastic. For example, electronic connectors.
Decorative purposes.

Knurling is obtained by the displacement of material as the knurling wheel is pressed against the surface of a rotating workpiece.

Knurling assembly — **For Better Assembly**

MicroMeter Knob — **For Better Assembly**

Knurling Wheels:

Knurling wheels are usually made from PVD-coated HSS.
The diameter is usually between 0.5 – 1.5 Inches (6 – 32 mm).
The pitch typically ranges between 8 to 80 TPI (3 – 0.5 mm)
They come in different patterns (See below).

Knurling comes in 4 main patterns:

Straight
Diamond
Diagonal Left
Diagonal Right

Unless otherwise specified Diamond and diagonal knurls are slanted 30°

There are two production technologies to obtain a knurl on a workpiece:

Knurl Forming:

The knurling wheel is pressed onto the rotating workpiece and displaces material.
This method is easy to implement.
The diameter of the workpieces changes depending on the pitch of the knurl, and the user needs to calculate the correct blank diameter to get the desired final diameter after knurling.
The forces are high, depending on the feed, diameter, and knurl’s width.
Low feeds.
Suitable for small-diameter parts.

Knurl Cutting:

The knurling wheels are tilted, moving along the axis of the workpiece, thus cutting instead of forming.
The cutting tool is more expensive, and implementation is more complicated.
No diameter change
Smaller forces.
Higher feeds.
The better solution for larger diameters.

Parameters dictionary

Pitch Parameters

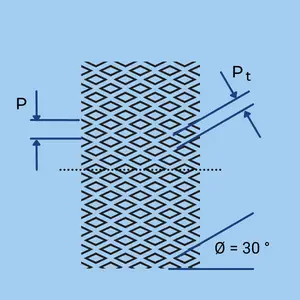
P – Circular Pitch: The distance between teeth, measured parallel to the knurl [mm / Inch].
P_t – Traverse Pitch: The distance between teeth, measured parallel to the workpiece/wheel axis [mm / Inc].
TPI Tooth per Inch: The pitch expressed as the number of teeth in one inch (25.4 mm)
Ø – Helix angle: The angle of the knurl line relative to the workpiece/wheel axis (Usually 30°)
Z – Number of teeth.
T_f– Tooth Factor: A factor used to calculate the number of teeth.

Diameter Parameters

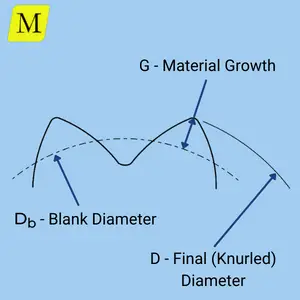
D – Final diameter after knurling: Usually, the drawing’s requirement since it is the functional dimension of the knurl.
D_b – The blank (or turned) diameter: The required diameter on the blank that is needed to receive the final diameter after the knurling operation. This is a technological parameter that you need to calculate.
G- Material Growth: The amount of material that is “pushed” by the knurling operation. It is an auxiliary parameter used to calculate the blank diameter.
D_w – Wheel diameter: The diameter of the knurling wheel.

Knurling calculations

Pitch Formulas:

\( \large P_t = \LARGE \frac{P}{\cos{\theta }} \large \text { [inch / mm]} \)
\( \large TPI_t = TPI \times \cos{\theta } \)
\( \large TPI = \LARGE \frac {1}{P} \large \text { (When the pitch is measured in Inches)} \)
\( \large TPI = \LARGE \frac {25.4}{P} \large \text { (When the pitch is measured in mm)} \)

\( \large P_t = \LARGE \frac{P}{\cos{\theta }} \large \text { [inch / mm]} \)
\( \large TPI_t = TPI \times \cos{\theta } \)
\( \large TPI = \LARGE \frac {1}{P} \)
\( \large TPI = \LARGE \frac {25.4}{P} \)

Diameter and tooth Formulas:

\( \large G = function (TPI) \text { [see chart and explanation below]} \)
\( \large D = D_b + 2 \times G \)
\( \large Z = T_f * TPI \times \pi \times D_b \)
\( \large T_f = function (TPI,Dw) \text { [see chart and explanation below]} \)

\( \large G = function (TPI) \)
\( \large D = D_b + 2 \times G \)
\( \large Z = T_f * TPI \times \pi \times D_b \)
\( \large T_f = function (TPI,Dw) \)

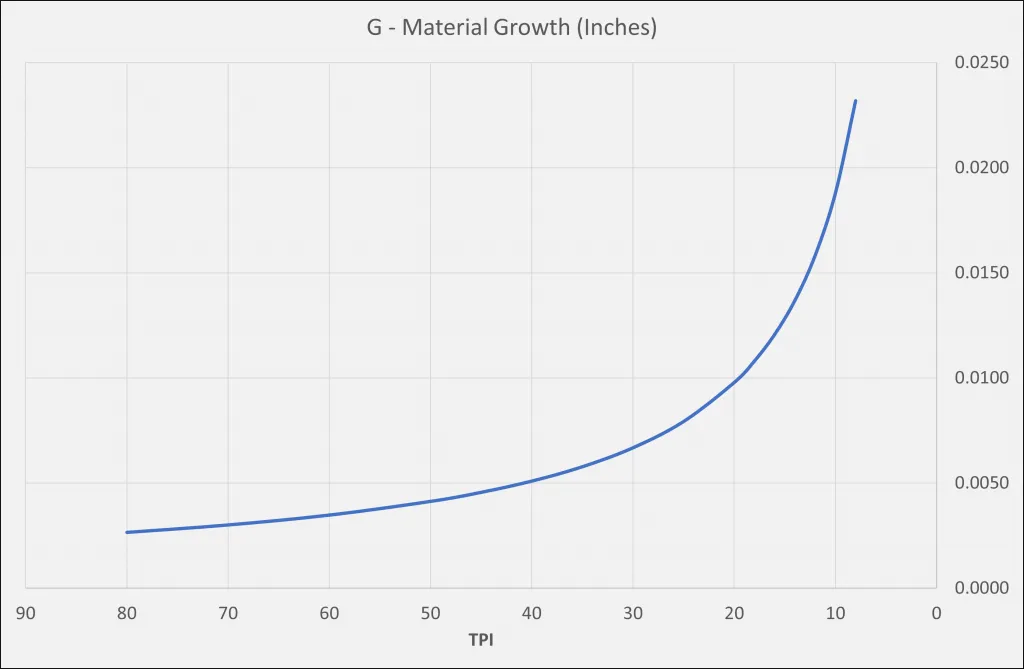
Material Growth (G) :

The knurling wheel “pushes” the material when the teeth are formed, thus enlarging the diameter. Therefore, the final diameter after knurling is larger than the diameter of the blank before the knurling operation.
The drawing of the part typically shows the final diameter after knurling.
However, to obtain it, you need to turn the part to a smaller diameter, yielding the required diameter after the knurling operation.
This can be done by trial and error, or by obtaining a good approximation of the Material Growth amount (G).
G is a function of the pitch, as shown in the below chart.
The chart is for straight knurls. For diamond-shaped knurls, the value should be increased by 15%.
Our Online Calculator, makes all these calculations for you!

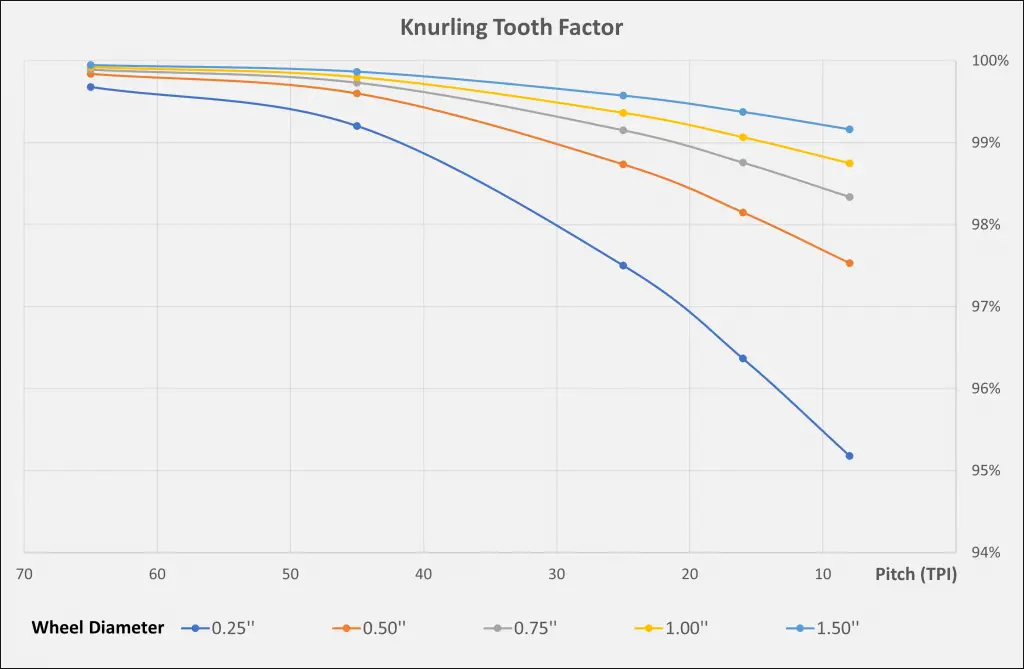
Number of Tooth Factor (Tf) :

The number of teeth that will form on the part depends on the pitch and its diameter.
When the pitch is given in TPI and the diameter in inches, it should equal TPI * Pi * Diameter.
However, in “real life”, this value should be multiplied by the Teeth Factor (TF), a function of the knurling wheel diameter and the pitch.
The below chart shows TF values for different wheel sizes.
As can be seen from the chart, the maximum error is 5%, and it gets smaller as the wheel diameter and the TPI increase.
The Online Calculator implements the tooth factor automatically in its algorithm.
The best practice is to obtain an integer number of teeth of the part. The calculator shows you the exact diameters that give such a result.
It is recommended to use this value (as long as it is within the allowed tolerance on the drawing).

Knurling Charts

Speeds and Feeds for knurling per Material Groups

Knurling Cutting Speeds Chart
Knurling Feeds – Inch
Knurling Feeds – Metric
Knurling Pitch (TPI) Chart

Knurling Cutting Speeds Chart

Material	Cutting Speed [SFM]	Cutting Speed [m/min]
Carbon Steel	50 - 70	15 - 20
Alloy Steel	35 - 50	10-15
Stainless Steel	35 - 50	10-15
Aluminum	90 - 125	30 - 40
Brass	90 - 125	30 - 40

Knurling Feeds – Inch

Filter Material:

Material	Pitch [TPI]	Circular Pitch [Inch]	In Feed [IPR]	Side Feed [IPR]
Carbon Steel	8	0.125	0.001 - 0.003	0.004 - 0.006
Carbon Steel	10	0.1	0.001 - 0.003	0.005 - 0.007
Carbon Steel	12	0.0833	0.001 - 0.003	0.005 - 0.007
Carbon Steel	14	0.0714	0.001 - 0.003	0.006 - 0.008
Carbon Steel	16	0.0625	0.002 - 0.004	0.006 - 0.009
Carbon Steel	20	0.05	0.002 - 0.004	0.007 - 0.01
Carbon Steel	25	0.04	0.002 - 0.004	0.008 - 0.011
Carbon Steel	30	0.0333	0.002 - 0.004	0.009 - 0.012
Carbon Steel	35	0.0286	0.002 - 0.004	0.009 - 0.012
Carbon Steel	40	0.025	0.002 - 0.004	0.01 - 0.013
Carbon Steel	50	0.02	0.002 - 0.004	0.01 - 0.014
Carbon Steel	80	0.0125	0.002 - 0.004	0.012 - 0.016
Alloy Steel	8	0.125	0.001 - 0.002	0.003 - 0.004
Alloy Steel	10	0.1	0.001 - 0.002	0.004 - 0.005
Alloy Steel	12	0.0833	0.001 - 0.002	0.004 - 0.006
Alloy Steel	14	0.0714	0.001 - 0.002	0.004 - 0.006
Alloy Steel	16	0.0625	0.001 - 0.003	0.005 - 0.007
Alloy Steel	20	0.05	0.001 - 0.003	0.005 - 0.007
Alloy Steel	25	0.04	0.001 - 0.003	0.006 - 0.008
Alloy Steel	30	0.0333	0.001 - 0.003	0.006 - 0.009
Alloy Steel	35	0.0286	0.001 - 0.003	0.007 - 0.009
Alloy Steel	40	0.025	0.001 - 0.003	0.007 - 0.01
Alloy Steel	50	0.02	0.001 - 0.003	0.008 - 0.01
Alloy Steel	80	0.0125	0.001 - 0.003	0.009 - 0.012
Stainless Steel	8	0.125	0.001 - 0.002	0.003 - 0.004
Stainless Steel	10	0.1	0.001 - 0.002	0.004 - 0.005
Stainless Steel	12	0.0833	0.001 - 0.002	0.004 - 0.006
Stainless Steel	14	0.0714	0.001 - 0.002	0.004 - 0.006
Stainless Steel	16	0.0625	0.001 - 0.003	0.005 - 0.007
Stainless Steel	20	0.05	0.001 - 0.003	0.005 - 0.007
Stainless Steel	25	0.04	0.001 - 0.003	0.006 - 0.008
Stainless Steel	30	0.0333	0.001 - 0.003	0.006 - 0.009
Stainless Steel	35	0.0286	0.001 - 0.003	0.007 - 0.009
Stainless Steel	40	0.025	0.001 - 0.003	0.007 - 0.01
Stainless Steel	50	0.02	0.001 - 0.003	0.008 - 0.01
Stainless Steel	80	0.0125	0.001 - 0.003	0.009 - 0.012
Aluminum	8	0.125	0.003 - 0.005	0.005 - 0.007
Aluminum	10	0.1	0.003 - 0.005	0.006 - 0.009
Aluminum	12	0.0833	0.003 - 0.005	0.007 - 0.01
Aluminum	14	0.0714	0.003 - 0.005	0.008 - 0.011
Aluminum	16	0.0625	0.004 - 0.008	0.008 - 0.011
Aluminum	20	0.05	0.004 - 0.008	0.009 - 0.013
Aluminum	25	0.04	0.004 - 0.008	0.01 - 0.014
Aluminum	30	0.0333	0.004 - 0.008	0.011 - 0.015
Aluminum	35	0.0286	0.004 - 0.008	0.012 - 0.016
Aluminum	40	0.025	0.004 - 0.008	0.012 - 0.017
Aluminum	50	0.02	0.004 - 0.008	0.013 - 0.018
Aluminum	80	0.0125	0.004 - 0.008	0.016 - 0.021
Brass	8	0.125	0.003 - 0.005	0.005 - 0.007
Brass	10	0.1	0.003 - 0.005	0.006 - 0.009
Brass	12	0.0833	0.003 - 0.005	0.007 - 0.01
Brass	14	0.0714	0.003 - 0.005	0.008 - 0.011
Brass	16	0.0625	0.004 - 0.008	0.008 - 0.011
Brass	20	0.05	0.004 - 0.008	0.009 - 0.013
Brass	25	0.04	0.004 - 0.008	0.01 - 0.014
Brass	30	0.0333	0.004 - 0.008	0.011 - 0.015
Brass	35	0.0286	0.004 - 0.008	0.012 - 0.016
Brass	40	0.025	0.004 - 0.008	0.012 - 0.017
Brass	50	0.02	0.004 - 0.008	0.013 - 0.018
Brass	80	0.0125	0.004 - 0.008	0.016 - 0.021

Knurling Feeds – Metric

Filter Material:

Material	Pitch [TPI]	Circular Pitch [mm]	In Feed [mm/Rev]	Side Feed [mm/Rev]
Carbon Steel	8	3.18	0.04 - 0.07	0.1 - 0.14
Carbon Steel	10	2.54	0.04 - 0.07	0.12 - 0.17
Carbon Steel	12	2.12	0.04 - 0.07	0.14 - 0.19
Carbon Steel	14	1.81	0.04 - 0.07	0.15 - 0.21
Carbon Steel	16	1.59	0.05 - 0.1	0.16 - 0.22
Carbon Steel	20	1.27	0.05 - 0.1	0.18 - 0.25
Carbon Steel	25	1.02	0.05 - 0.1	0.2 - 0.27
Carbon Steel	30	0.85	0.05 - 0.1	0.22 - 0.3
Carbon Steel	35	0.73	0.05 - 0.1	0.23 - 0.31
Carbon Steel	40	0.64	0.05 - 0.1	0.24 - 0.33
Carbon Steel	50	0.51	0.05 - 0.1	0.26 - 0.35
Carbon Steel	80	0.32	0.05 - 0.1	0.3 - 0.41
Alloy Steel	8	3.18	0.02 - 0.04	0.08 - 0.11
Alloy Steel	10	2.54	0.02 - 0.04	0.09 - 0.13
Alloy Steel	12	2.12	0.02 - 0.04	0.1 - 0.14
Alloy Steel	14	1.81	0.02 - 0.04	0.11 - 0.15
Alloy Steel	16	1.59	0.04 - 0.07	0.12 - 0.17
Alloy Steel	20	1.27	0.04 - 0.07	0.14 - 0.19
Alloy Steel	25	1.02	0.04 - 0.07	0.15 - 0.21
Alloy Steel	30	0.85	0.04 - 0.07	0.16 - 0.22
Alloy Steel	35	0.73	0.04 - 0.07	0.17 - 0.23
Alloy Steel	40	0.64	0.04 - 0.07	0.18 - 0.25
Alloy Steel	50	0.51	0.04 - 0.07	0.2 - 0.27
Alloy Steel	80	0.32	0.04 - 0.07	0.23 - 0.31
Stainless Steel	8	3.18	0.02 - 0.04	0.08 - 0.11
Stainless Steel	10	2.54	0.02 - 0.04	0.09 - 0.13
Stainless Steel	12	2.12	0.02 - 0.04	0.1 - 0.14
Stainless Steel	14	1.81	0.02 - 0.04	0.11 - 0.15
Stainless Steel	16	1.59	0.04 - 0.07	0.12 - 0.17
Stainless Steel	20	1.27	0.04 - 0.07	0.14 - 0.19
Stainless Steel	25	1.02	0.04 - 0.07	0.15 - 0.21
Stainless Steel	30	0.85	0.04 - 0.07	0.16 - 0.22
Stainless Steel	35	0.73	0.04 - 0.07	0.17 - 0.23
Stainless Steel	40	0.64	0.04 - 0.07	0.18 - 0.25
Stainless Steel	50	0.51	0.04 - 0.07	0.2 - 0.27
Stainless Steel	80	0.32	0.04 - 0.07	0.23 - 0.31
Aluminum	8	3.18	0.07 - 0.13	0.14 - 0.18
Aluminum	10	2.54	0.07 - 0.13	0.16 - 0.22
Aluminum	12	2.12	0.07 - 0.13	0.18 - 0.24
Aluminum	14	1.81	0.07 - 0.13	0.2 - 0.27
Aluminum	16	1.59	0.11 - 0.2	0.21 - 0.29
Aluminum	20	1.27	0.11 - 0.2	0.24 - 0.32
Aluminum	25	1.02	0.11 - 0.2	0.26 - 0.36
Aluminum	30	0.85	0.11 - 0.2	0.28 - 0.38
Aluminum	35	0.73	0.11 - 0.2	0.3 - 0.41
Aluminum	40	0.64	0.11 - 0.2	0.32 - 0.43
Aluminum	50	0.51	0.11 - 0.2	0.34 - 0.46
Aluminum	80	0.32	0.11 - 0.2	0.39 - 0.53
Brass	8	3.18	0.07 - 0.13	0.14 - 0.18
Brass	10	2.54	0.07 - 0.13	0.16 - 0.22
Brass	12	2.12	0.07 - 0.13	0.18 - 0.24
Brass	14	1.81	0.07 - 0.13	0.2 - 0.27
Brass	16	1.59	0.11 - 0.2	0.21 - 0.29
Brass	20	1.27	0.11 - 0.2	0.24 - 0.32
Brass	25	1.02	0.11 - 0.2	0.26 - 0.36
Brass	30	0.85	0.11 - 0.2	0.28 - 0.38
Brass	35	0.73	0.11 - 0.2	0.3 - 0.41
Brass	40	0.64	0.11 - 0.2	0.32 - 0.43
Brass	50	0.51	0.11 - 0.2	0.34 - 0.46
Brass	80	0.32	0.11 - 0.2	0.39 - 0.53

knurling Pitch (TPI) Chart

TPI	Pitch (Inch)	Pitch (mm)
8	0.1250	3.18
10	0.1000	2.54
12	0.0833	2.12
14	0.0714	1.81
16	0.0625	1.59
20	0.0500	1.27
25	0.0400	1.02
30	0.0333	0.85
35	0.0286	0.73
40	0.0250	0.64
50	0.0200	0.51
60	0.0167	0.42
80	0.0125	0.32

Related Glossary Terms:

SpeeDoctor

ThreaDoctor

Each Data-Sheet Includes:

Convert material standards:

SpeeDoctor

ThreaDoctor

Each Data-Sheet Includes:

Convert material standards:

Knurling calculator, charts, and formulas

Knurling Calculator