Planeado: Calculadora de tiempo de ciclo y fórmulas

Calcular el tiempo de ciclo de las operaciones de Planeado, Tronzado y Ranurado profundo es complicado porque:

La velocidad del cabezal cambia constantemente.
En algún momento del proceso, las RPM máximas de la máquina limitan la velocidad de corte.

Más información

Calculadora Online

Calculadora de tiempo de ciclo de Planeado, Tronzado y Ranurado profundo

Fórmulas de tiempo de ciclo de Planeado, Tronzado y Ranurado profundo

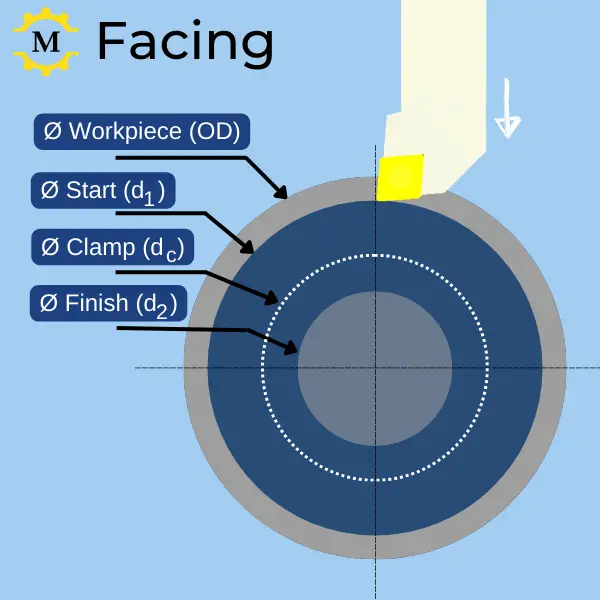
_d1 – Diámetro inicial
_d2 – Diámetro final
_nmax – RPM máximas de la máquina.
_Vc – Velocidad de corte
f – Velocidad de avance
dc_– Diámetro de sujeción: El diámetro en el que la velocidad máxima del husillo de la máquina limita la velocidad de corte (ver más abajo).
t₁ – Tiempo de ciclo por encima del diámetro de sujeción.
t₂ – Tiempo de ciclo por debajo del diámetro de sujeción.
T – Duración total del ciclo

Unidades:

Tiempos en minutos.
Diámetros en pulgadas o milímetros.
Velocidad de corte en SFM de metros/minuto.
Avance en IPR o milímetros por revolución

El cálculo del tiempo de funcionamiento del torneado longitudinal es sencillo, ya que el diámetro es constante. Por lo tanto, las velocidades de corte y del husillo también permanecen constantes durante toda la operación, y se aplica la sencilla fórmula siguiente. (Donde l es la distancia a girar)

\( \large T = \Large \frac{l}{f \times n}\)

En el Planeado, Tronzado y Ranurado, el diámetro cambia constantemente, y el tiempo total de corte debe calcularse mediante una integral.

\( \large t_1 = \Large \int_{d_1}^{d_2} \large T(d) = \pi \times \Large \frac{d_1^2\,-\,d_2^2}{12 \times f \times V_c } \)

En unidades métricas, la constante 12 debe sustituirse por 1,000

La situación se complica porque cada máquina tiene una limitación de velocidad máxima del husillo (_nmax). Para mantener la velocidad de corte (_Vc), la velocidad del cabezal (n) aumenta a medida que la máquina pasa de _d1 a _d2.

\( \large n = \Large \frac{12 \times V_c}{\pi \times d} \)

En unidades métricas, la constante 12 debe sustituirse por 1,000

En un determinado diámetro del camino, n alcanzará _nmáx. Este diámetro se denomina «diámetro de sujeción» (_dc), ya que a partir de este diámetro, la velocidad del husillo está «sujeta», y la velocidad de corte empieza a disminuir.

\( \large d_c = \Large \frac{12 \times V_c}{\pi \times n_{max}} \)

En unidades métricas, la constante 12 debe sustituirse por 1,000

La primera fórmula para _t1 sólo es válida para diámetros mayores que el diámetro de sujeción. Para diámetros inferiores al diámetro de sujeción se aplica una fórmula diferente y más sencilla.

\( \large t_2 = \Large \frac{d_1\,-\,\,d_2}{2\,\times\,f\,\times\,n_{max}} \)

Resumen

Para realizar el cálculo correcto, debe identificar su situación en relación con el diámetro de sujeción.

Caso 1: Tanto el diámetro inicial como el final son mayores que el diámetro de sujeción.
Caso 2: El diámetro de sujeción se encuentra entre los diámetros inicial y final.
Caso 3: Tanto el diámetro inicial como el final son menores que el diámetro de sujeción.

Fórmulas para el caso 1:

\( \large T = t_1 = \Large \pi \times \Large \frac{d_1^2\,-\,\,d_2^2}{12 \times f \times V_c } \)

Fórmulas para el caso 2:

\( \large T = t_1 + t_2 = \Large \pi \times \Large \frac{d_1^2\,-\,\,d_c^2}{12 \times f \times V_c } + \frac{d_c\,-\,\,d_2}{2\,\times\,f\,\times\,n_{max}}\)

\( \bbegin{array}{l} \large T = t_1 + t_2 = \\ \Large \pi \times \Large \frac{d_1^2\,-\,\,d_c^2}{12 \times f \times V_c } \\ \Large\,+\, \frac{d_c\,-\,\,d_2}{2\,\times\,f\,\times\,n_{max}} \end{array}\)

Formulas para el Caso 3:

\( \large T = t_2 = \Large \frac{d_1\,-\,\,d_2}{2\,\times\,f\,\times\,n_{max}} \)