Adelgazamiento de virutas: Calculadoras y fórmulas

¿Qué es el adelgazamiento de virutas?

En una operación de fresado «Clásica», la profundidad de corte radial [Ae] es mayor o igual que el radio de la fresa, y el ángulo es de 90°. En estos casos, la carga de viruta es igual al avance por diente.

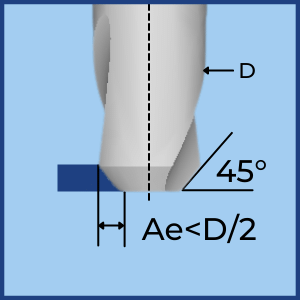
Cuando la profundidad de corte radial [Ae] es menor que el radio del fresado, o la forma de la fresa no es de 90° (chaflán, nariz de bola, etc.), la carga de viruta es menor que el avance por diente. Esta reducción de la carga de virutas se denomina «adelgazamiento de virutas».

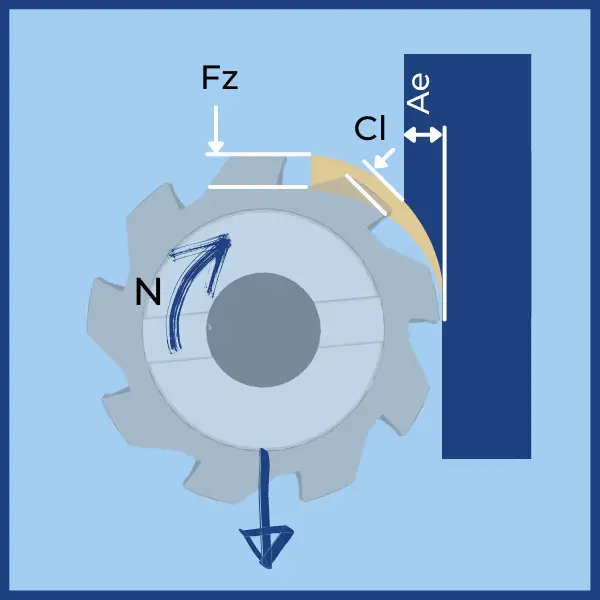
La relación entre la carga de viruta [CL] y el avance por diente [Fz] está representada por elFactor Adelgazamiento de virutas [CTF]

\( \large CTF = \frac {\huge F_z}{\huge C_l} \)

Calculadora de adelgazamiento radial de virutas

Calculadora de adelgazamiento axial de virutas

Explicación del adelgazamiento de virutas

La carga de viruta (espesor máximo de viruta) es uno de los parámetros más importantes para conseguir un proceso de fresado productivo y fiable. Sólo se obtendrá un corte eficaz cuando la carga de viruta esté en el rango correcto apropiado para una cortadora específica. La mejor práctica es obtenerlo del catálogo del proveedor, pero si no lo tiene, puede utilizar nuestra Calculadora de carga de virutas, que le dará un buen punto de partida.

• Una Carga de Viruta (Espesor Máximo de Viruta) demasiado baja puede provocar un rendimiento deficiente debido al rozamiento, con la consiguiente pérdida de vida útil de la herramienta o formación de viruta.
• Una carga de viruta demasiado elevada sobrecargará el filo de corte, provocando un desgaste rápido e incluso la rotura.

El factor de adelgazamiento de viruta (CTF) permite calcular el avance por diente que producirá la carga de viruta deseada.

Hay dos factores de adelgazamiento de virutas:

• RCTF – Factor de adelgazamiento radial de la viruta.
• ACTF – Factor de adelgazamiento axial de virutas.

Los dos factores son independientes y deben aplicarse uno encima del otro:

\( \large CTF = RTCF \times ACTF \)
\( \large F_z= Recomended \ Chip \ Load * CTF \)

Adelgazamiento radial de virutas

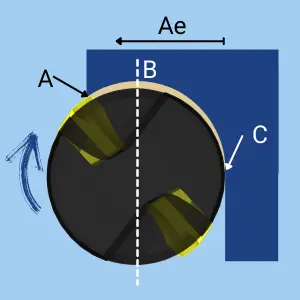
• En una operación de fresado, el espesor de viruta varía entre el punto de entrada (A) y el punto de salida (C).
• En el Punto de Salida (C), el espesor es siempre Cero.
• Cuando la profundidad de corte radial (Ae) es mayor que el radio de la fresa, el espesor de la viruta comienza con un valor determinado. Crece gradualmente hasta alcanzar su espesor máximo en el centro de la cuchilla (B). En este punto, el Espesor máximo de viruta es igual al Avance por diente.
• Después, el espesor de la viruta disminuye progresivamente hasta llegar a cero en el punto de salida (C).

Fórmulas de adelgazamiento radial de virutas

• Fz – Alimentación por diente. El objetivo es calcular la Fz que creará la Carga de viruta recomendada.
• Cl – Carga de la Viruta. (Recomendado por el proveedor de herramientas o a partir de nuestra Calculadora de carga de virutas).
• Ae – Profundidad de corte radial.
• D – Diámetro efectivo de la Fresa.
• RCTF – Factor de adelgazamiento radial de la viruta. La relación entre la carga de viruta (Cl) y el avance por diente (Fz)

\( \large RCTF = \frac {\huge 1}{\huge \sqrt{1 – \left [ 1 – \frac {2 \times A_e}{D} \right ]^{2}}} \)

\( \large F_z = RCTF \times C_l \)

Adelgazamiento axial de virutas

Cuando el filo de corte se aproxima al material en un ángulo de 90°, el avance por diente [Fz] es igual a la carga de viruta (espesor de viruta). [Cl]

Cuando el filo de corte se aproxima al material en un ángulo inferior a 90°, el Avance por diente [Fz] es mayor que la Carga de viruta (Espesor de viruta). [Cl]

El mismo principio funciona también con los filos redondos (como las fresas de punta esférica y las fresas con plaquitas redondas). En estos casos, el ángulo de aproximación es la tangente al radio del filo de corte en el punto más profundo de enganche.

Observación importante: El término «adelgazamiento axial de virutas» es engañoso. Se debe a que en una fresa redonda el adelgazamiento de la viruta es función de la profundidad axial. Sin embargo, como se ha explicado anteriormente, en realidad es el resultado del ángulo de aproximación. En las fresas de avance y las fresas de chaflán, la profundidad axial no influye en el espesor de la viruta. Un término más apropiado sería «Ángulo de aproximación de Adelgazamiento de virutas». Sin embargo, para ser coherentes con el apodo común nos referimos a ella como «Adelgazamiento Axial de Virutas».

Fórmulas de adelgazamiento axial de virutas

Fresas de chaflán

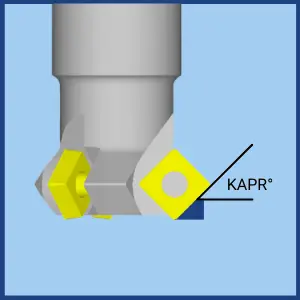
• Fz – Alimentación por diente. El objetivo es calcular la Fz que creará la Carga de viruta recomendada.
• Cl – Carga de la Viruta. (Recomendado por el proveedor de herramientas o a partir de nuestra Calculadora de carga de virutas).
• KAPR – Ángulos de Aproximación
• ACTF – Factor de adelgazamiento axial de la viruta. La relación entre la carga de viruta (Cl) y el avance por diente (Fz)

\( \large ACFT = \huge \frac { 1}{\sin { \left ( kapr \right )}} \)

\( \large F_z = ACFT \times C_l \)

Fresas de punta esférica

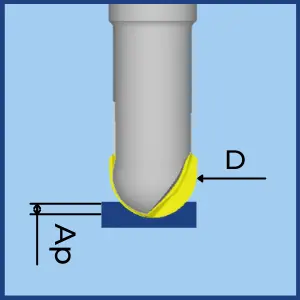
• Fz – Alimentación por diente. El objetivo es calcular la Fz que creará la Carga de viruta recomendada.
• Cl – Carga de la Viruta. (Recomendado por el proveedor de herramientas o a partir de nuestra Calculadora de carga de virutas).
• Ap- Profundidad de corte
• D – Diámetro de la bola.
• ACTF – Factor de adelgazamiento axial de la viruta. La relación entre la carga de viruta (Cl) y el avance por diente (Fz)

\( \large ACFT = \frac {\huge D}{\sqrt{\huge D^{2} \ – \ {\left [ D \ – \ 2 \ \times \ Ap\right ]}^2}} \)

\( \large F_z = ACFT \times C_l \)

Cortadores de plaquita redonda

• Fz – Alimentación por diente. El objetivo es calcular la Fz que creará la Carga de viruta recomendada.
• Cl – Carga de la Viruta. (Recomendado por el proveedor de herramientas o a partir de nuestra Calculadora de carga de virutas).
• Ap- Profundidad de corte
• IC – Tamaño del inserto (círculo inscrito.)
• ACTF – Factor de adelgazamiento axial de la viruta. La relación entre la carga de viruta (Cl) y el avance por diente (Fz)

\( \large ACFT = \frac {\huge 1}{\sqrt{\huge \ \frac{4 \times ap}{IC} \ – \ {\left [ \frac{2 \times ap}{IC} \right ]}^2}} \)

\( \large F_z = ACFT \times C_l \)